决策树的直观解释
决策树就是通过一系列的特征来判断其属性,我们以苹果为例。
在买苹果的时候,我们会通过苹果的颜色、硬度、香味来判断是不是好苹果。例如我们有以下的数据:
| 颜色 | 硬度 | 香味 | 结论 | |
|---|---|---|---|---|
| 1 | 红色 | 硬 | 香 | 是 |
| 2 | 红色 | 硬 | 无味 | 是 |
| 3 | 红色 | 软 | 无味 | 否 |
| 4 | 绿色 | 软 | 无味 | 否 |
| 5 | 绿色 | 硬 | 香 | 是 |
| 6 | 绿色 | 硬 | 无味 | 否 |
那么,如果现在我们有一个红色、硬且有香味的苹果,我们就可以认为它为好苹果,因为它和我们的第一条数据想符合。那么如果存在一个苹果,它的属性组合不在我们拥有的数据内,我们怎么办呢?例如,我们有一个绿色、硬且无味的苹果。这时候我们就要考虑和其最近的情况。通过颜色来筛选,我们找到了3、4两条,然后通过硬我们找到了第三条,虽然香味两者不一样,但是基于我们的数据,我们可以基本认为两者是非常接近的,所以我们会认为它是好苹果。这时候就有一个问题了,为什么不选择第4条为最近的呢,他们也有两个属性是相同的。这里我们就要考虑到属性的优劣了,这会在后面讲到。
基于上面的数据,我们可以构建如下的决策树:
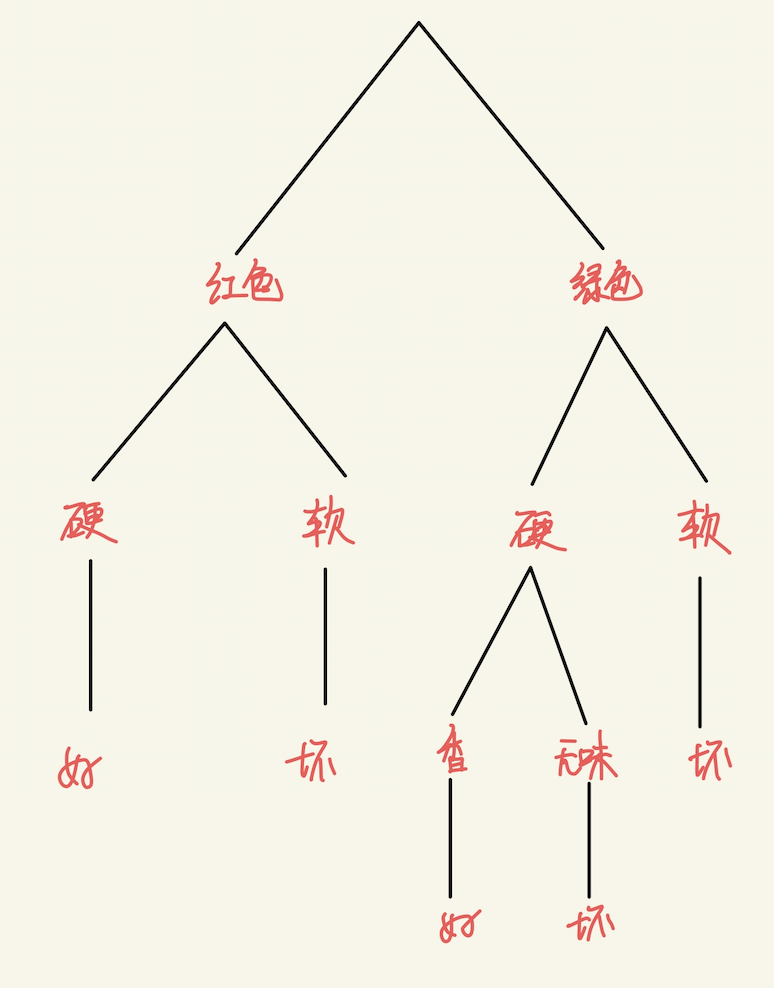
图中有一点需要注意,就是红色、硬后面我们没有对其用香味来判断,因为无论香与否,结论都是好苹果。
决策树的数学视角
在《统计学习方法》中,详细定义了决策树。
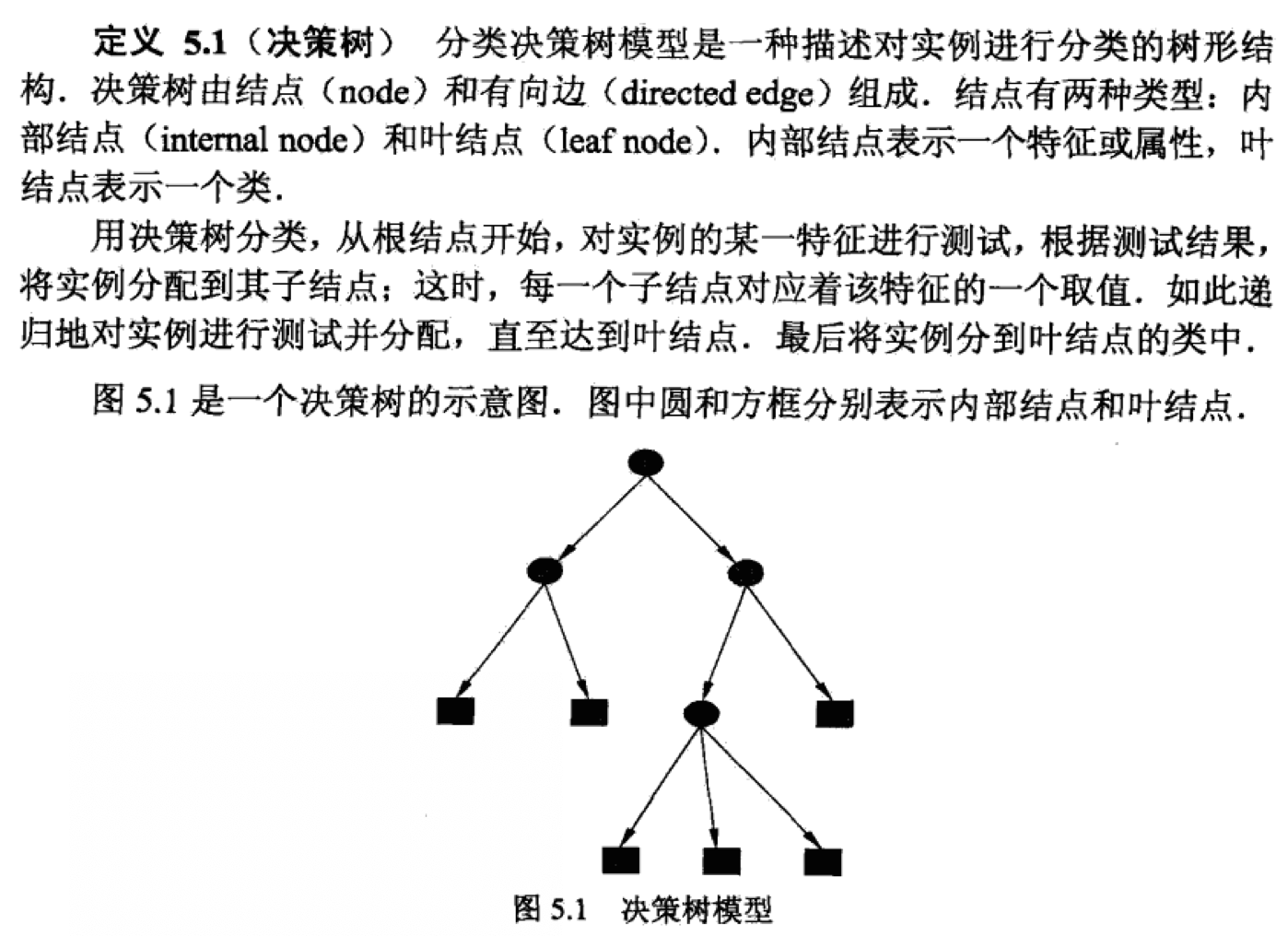
显然,决策树构建中,特征属性选择是最为关键的,我们希望选取对悬链数据具有分类能力的特征。这时候,引进熵的相关概念。熵是用来表示随机变量不确定性的度量。假如我们有个随机变量,其概率分布为
那么,我们就可以定义变量X的熵
熵越大,随机变量的不确定性也越大。并且。
假设随机变量的联合概率分布为
那么,我们可以定义条件熵
基于上面两个定义,我们就可以引出信息增益和信息增益比的概念。
信息增益就是度量根据变量A划分前后,数据集的混乱程度差别,如下
信息增益比就是就是信息增益与变量A的熵之比,如下
其中,

