一. 硬间隔SVM
直观感受
对于线性可分的数据,在感知机那一块,我们知道感知机无法确定一个唯一的超平面,随着$w, b$的初始化值得不同,最终得到的超平面也有可能不同。这是首我们就要考虑添加一个限制条件来求得一个唯一的超平面。掏出我们之前的那张图:
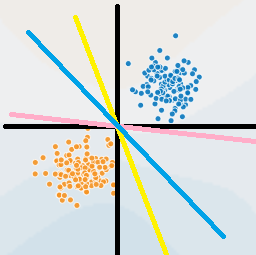
直观上,我们会觉得图中 的蓝色超平面优于黄色和红色,因为相较于其他两条直线,蓝色离两个数据簇都较远,直观上蓝色会更加稳定。
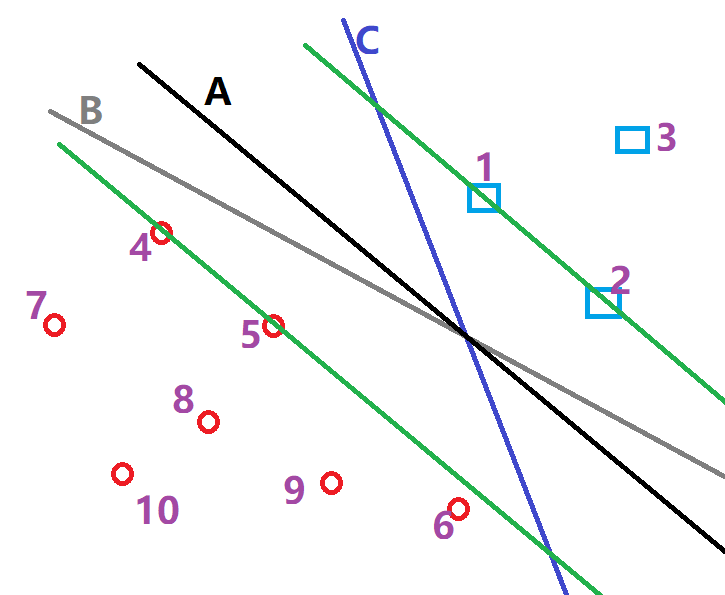
现在考虑寻找下图中的最优平面,和前面的一样,我们会认为超平面A优于其他两个,因为A与两个数据簇较远。例如超平面C就与点1离的太近。现在我们可以考虑给予这样的限制:两个数据簇中,离超平面最近的那个点的距离要足够大。例如,对于超平面C来说,我们希望蓝色数据簇中的点1离超平面足够大,红色数据簇中点6离超平面A足够大。
数学视角
为了找到一个这样的超平面,我们又要回到感知机中的点到超平面的距离的定义。
函数间隔公式:
几何间隔公式:
对于我们的超平面来说,和是完全一样的,但是在计算函数间隔的时候,这就会对我们造成困扰,距离会放大两倍。所以我们采用几何间隔来规范化距离。同时,为了之后求解的方便,我们去掉绝对值,
现在,考虑到我们要找到某个数据簇离超平面的最小距离,定义
为了找到最优的超平面,我们希望尽可能的大,所以最终我们有以下的优化问题:
对上面的优化问题进行改写,采用函数间隔,
更进一步来说,如果我们对放大倍,那么我们的优化问题变为
不难发现,我们的优化问题(7)和(6)是完全一样的,函数间隔的倍数改变对优化问题不产生影响。因此,我们令, 并且最大化和最小化 是等价的,所以最终我们有以下的优化条件,
这就是硬间隔SVM的原始问题。
为了求解这个最优化问题,考虑其对偶问题。首先我们定义其lagrange函数:
这时候,原始问题就变为了。其对偶问题就为。
现在,我们可以先求极小值,。对其分别求导,带入原式,我们可以得到最终的对偶问题。

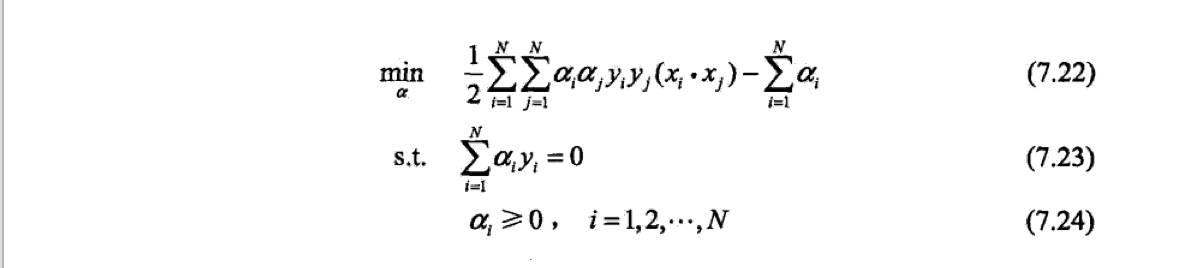
据此,我们得到了其对偶问题,同时,我们有以下定理

基于上面的定理,我们可以将我们的分类决策函数写为。
在上面的推导过程中,我们可以得知,并且
不难发现,和只与数据中所对应的数据点有关。而且这些数据点决定了我们最终得到的超平面,因此我们把这些数据点叫做支持向量。
到这里为止,已经基本阐述清楚对于线性可分数据的SVM的由来。但是对于线性不可分数据,我们怎么办?
二. 软间隔SVM
直观感受
通常,数据非线性可分常常是由于部分异常点造成的。去除这些异常点之后,数据往往是线性可分的。
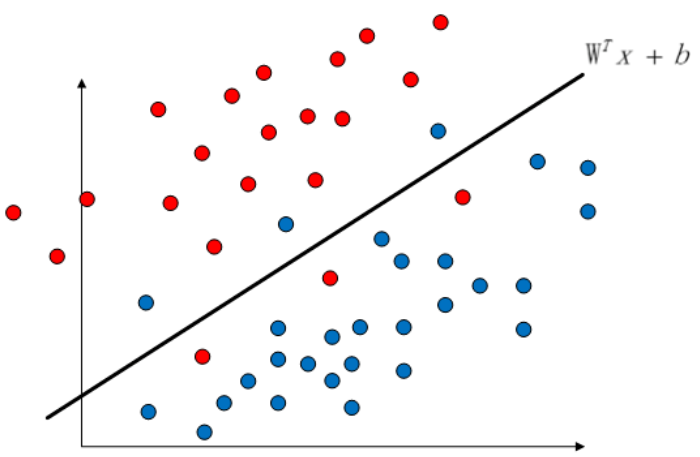
在上图中,我们可以看到如果我们去除超平面左侧区域的三个蓝色点,去除右侧区域的三个红色点,那么这个超片面就可以完美的将数据划分开了。因此,在这种情况下,我们无法用原来的约束来求得一个超平面,我们考虑修改约束条件。这时候,我们引进一个松弛变量。
数学视角
引进松弛变量的原因是在线性不可分数据的情况下,原问题的约束条件无法满足,即不能保证所有数据点到分离超平面的函数间隔都大于等于1。这时候如果我们引入一个松弛变量, 使得松弛变量和函数间隔之和大于等于1,这样所有数据就又满足了原来的约束条件。
正式来说,对于软间隔SVM,我们原始优化问题是:
上式中,是我们的惩罚项,即我们不能无限的放宽限制条件来容忍噪声。是我们的调和系数,通过它我们可以控制我们对噪声的容忍程度,当C较大的时候,松弛变量就会缩小。
与硬间隔的SVM相比,我们发现软间隔只是添加了一个额外的松弛变量,因此对于其对偶问题,我们可以通过相同的方法快速求得:
类似的,我们可以求得
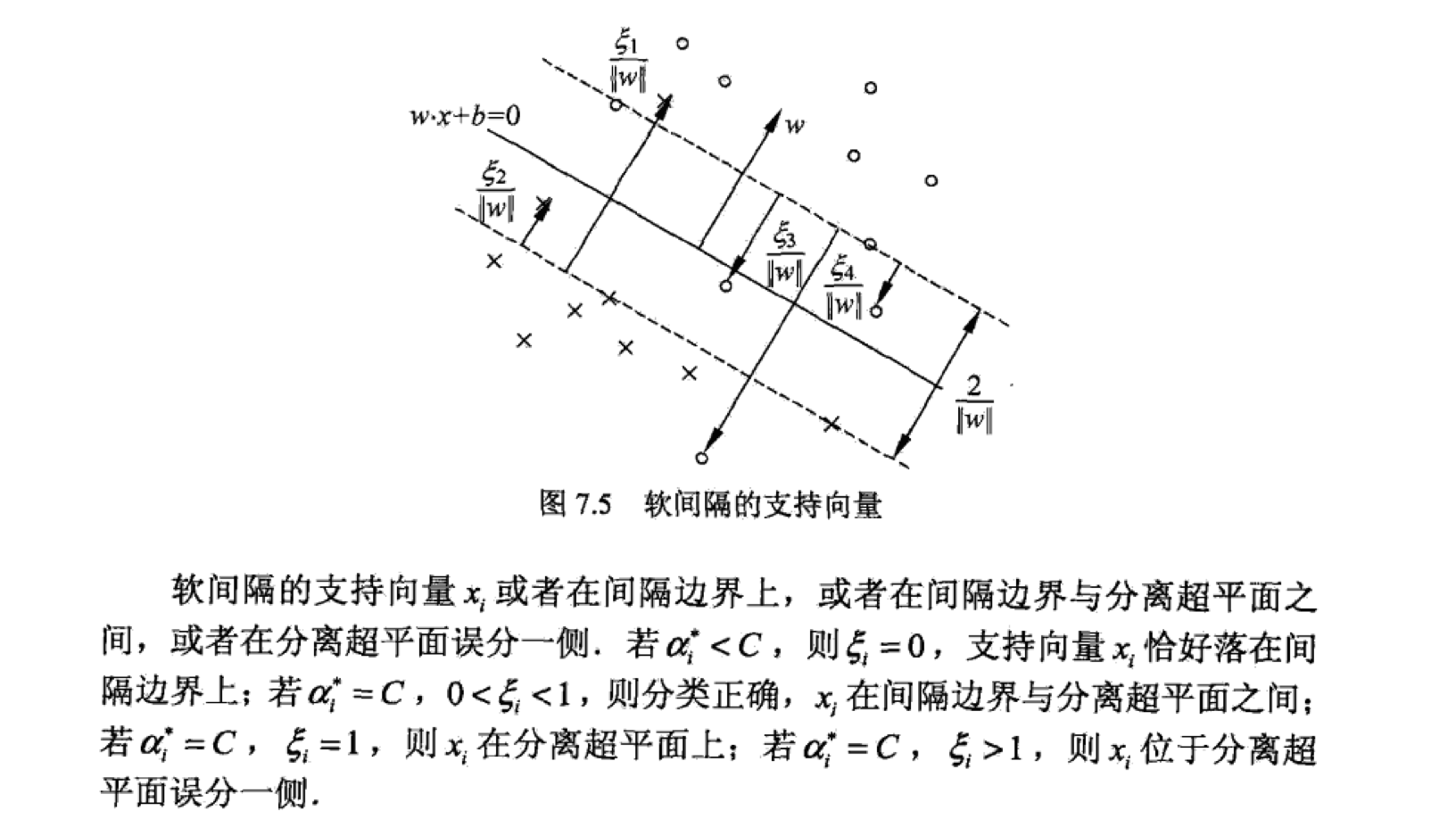
对于硬间隔SVM,我们知道对应的数据点是支持向量。对于软间隔SVM的支持向量,情况略微复杂。下图中标了距离的都是支持向量。
合页函数
SVM还有另外一个解释,即考虑,其中。对于目标函数的第一项,如果我们正确分类数据点,但是其到超平面的距离小于1,那么我们依旧有损失。只有当数据正确分类且到超平面的距离大于等于1,第一项才为0。第二项为正则项。
与原始SVM最优化问题的联系:
基于上面对于目标函数的分析,我们可以看出第一项就是软间隔SVM里面的松弛变量。同时如果我们假定, 那么我们就有。
Kernel
直观感受
对于上面的硬间隔SVM和软间隔SVM,我们的对象都是线性可分数据或者近似线性可分数据。那么对于非线性可分数据呢?这时候为了使用SVM,我们需要考虑核函数(Kernel)。直观上,核函数就是一种映射,将原本线性不可分的数据映射到另一个空间,从而线性可分。通俗来讲,就是变化坐标系。如下图:
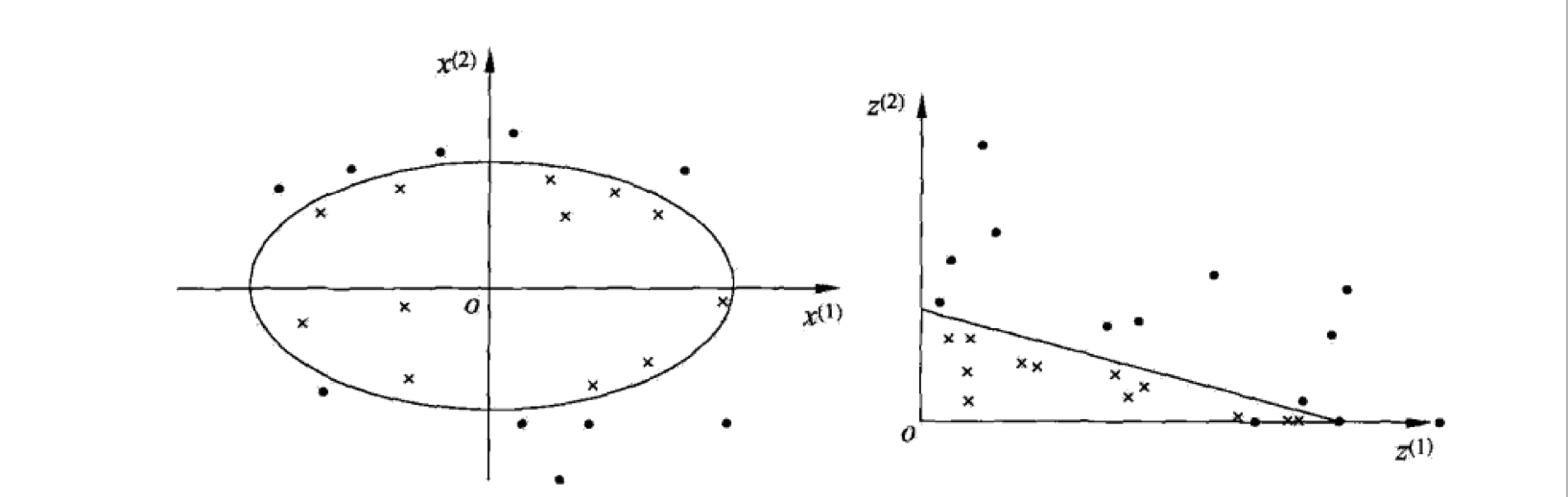
对于原数据,在原坐标系下面,是无法通过一个超平面将其划分开来的。但是我们可以看到可以用一个超曲面,这里为椭圆,将数据划分开。通过变换坐标系,我们可以看到右图中的数据线性可分了。
数学视角
那么到底什么是核函数?怎么定义核函数?


从上面的定义,我们可以看到对于一个核函数,其可以有不同的映射函数和特征空间,因此对于我们使用来说会很不方便。实际上,在使用核函数技巧的时候,我们都是直接定义和使用核函数,而不考虑其具体的映射函数和特征空间。
回忆支持向量机的对偶形式,其中包含了输入实例和实例的内积,核函数就应用在这个内积上。对偶问题的目标函数和决策函数为:
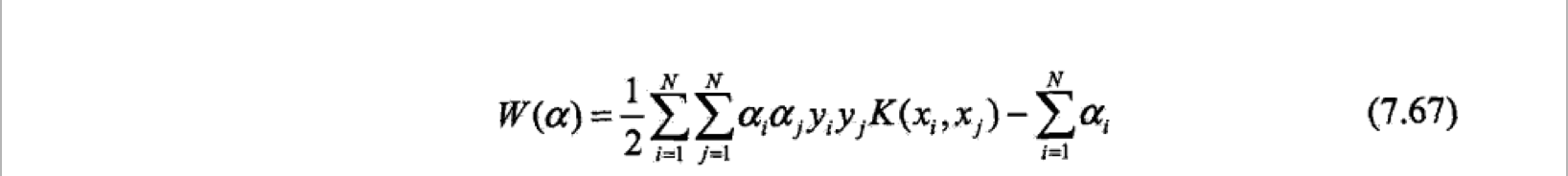
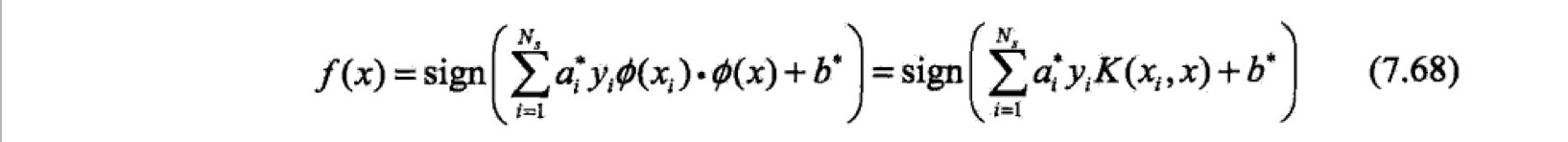
常用核函数:

序列最小最优化问题(SMO)
直观理解
SMO是高效实现SVM的一种方法。
首先考虑软间隔SVM的对偶问题。
其中,每一个对应一个数据点。所以变量的数据等于样本的数目。
由KKT我们可以得知,如果这个问题有最优解,那么他肯定满足KKT条件。如果不是最优解,那么可能无法满足KKT条件。但是同时考虑N个变量的最优化问题会非常复杂,且很难直接求解。
这时候我们就可以考虑SMO算法。SMO算法选择了其中两个为变量,固定了其他所有的变量,所以问题就变为了一个二次规划问题。选择两个的原因是对偶问题的一个限制条件是,如果只有一个是变量,那么其实他直接可以由其他的解出来,就无法优化了。
另一个角度考虑,这个二次规划问题的解肯定会使目标函数减小,从而二次规划问题的解也会更加靠近最优解。
数学理解
不是一般性,我们可以考虑和为变量,固定其他所有的变量。对(14)进行改写,
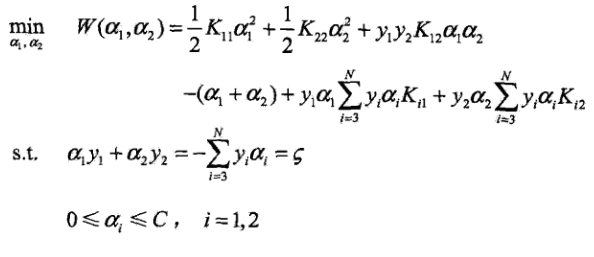
上面的优化问题的限制条件告诉我们,, 即是存在边界的,因此当我们计算得到最优的的时候,还要考虑其边界问题。因为只有两个变量,且都有范围,可以用二维平面图来解释。
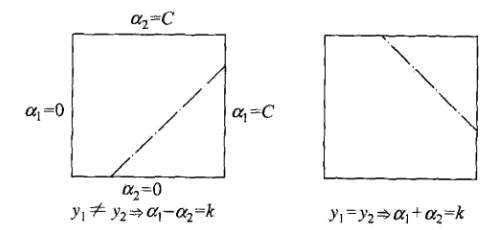
由于我们固定了其他变量,并且,最优化问题的解就在一条与对角线平行的线段上。变量的便捷点我们也可以很快的就求出来。

同时,我们可以求得优化问题的迭代公式

变量选择
第一个变量,我们选择违反KKT条件最严重的点。
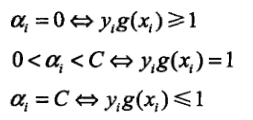
第二个变量选取的宗旨是使得最大。
具体可见李航的统计学原理P129。
代码实现
….未完待续….