感知机的直观感受
感知机是机器学习中的最基本也是最简单的一个算法。下图就是一个例子。
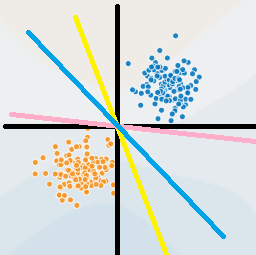
例如,我们有一个二维数据,横轴为$X_1$, 纵轴为$X_2$。图中有黄蓝红三条直线,都可以将两簇数据完美划分。其实,这三条直线就是感知机的分割线。如果数据是n维的,那就是分离超平面了。
并且我们需要注意到,感知机是没有一个确定解的。因为我们的目标只是将两个数据簇分开。如果想要确定一个唯一的超平面,那需要加限制条件,这将是SVM的内容。
感知机的数学视角
对于这样一个模型,我们怎么来找到一个超平面呢?
首先,如前面所说,感知机是依靠超平面来划分数据集的。数学上,我们定义超平面为 ,其中$w$为超平面的法向量,$b$为超平面的偏置。同时,由于我们需要通过这个超平面来划分数据,而我们的数据的标志, 因此我们定义函数为,其中
现在,我们考虑如何来确定损失函数。我们的目标是将数据点正确的划分,因此我们可以考虑数据点到超平面的距离来度量。距离公式为
考虑所有误分类点的集合$M$, 对于在$M$中的数据点,如果, 那么。反过来,如果, 那么. 因此我们可以通过乘以来去掉距离中的绝对值,因为绝对值的存在会妨碍我们优化模型。现在定义距离为
所以,我们的损失函数为
考虑到我们的数据是线性可分的,最终。因此,为了是优化更加简单,我们定义损失函数为
现在,考虑如何优化损失函数。我们采用随机梯度下降法(SGD), 首先对损失函数求导
随机选择一个, 更新权重
最后进行迭代直到损失函数为0。

感知机的对偶形式
对偶形式的思想就是用的线性组合来表示。考虑在初始化参数的时候,将设为0,由之前的迭代算法可知,
设总共修改了次参数,对于样本点,的增量分别是, 其中。
如果我们假定, 则,即表示第个实例点由于误分总共迭代更新的次数。
从中,我们可以得出,如果某个实例点更新的次数越多,它里超平面的距离也就越近,也就越难正确分类,它对最后确定的超平面的影响也就越大。
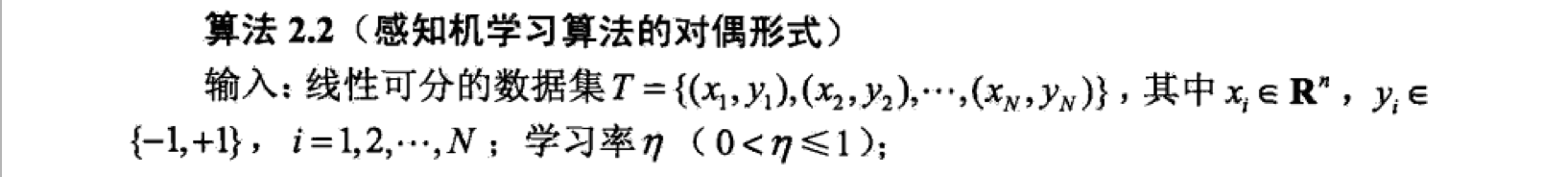

其中,, 加的原因是因为。误分一次,增加一个。
同时,由于存在实例之间内积,可以先计算Gram矩阵,存储所有的实例的之间的内积。
Python实现
1 | import numpy as np |